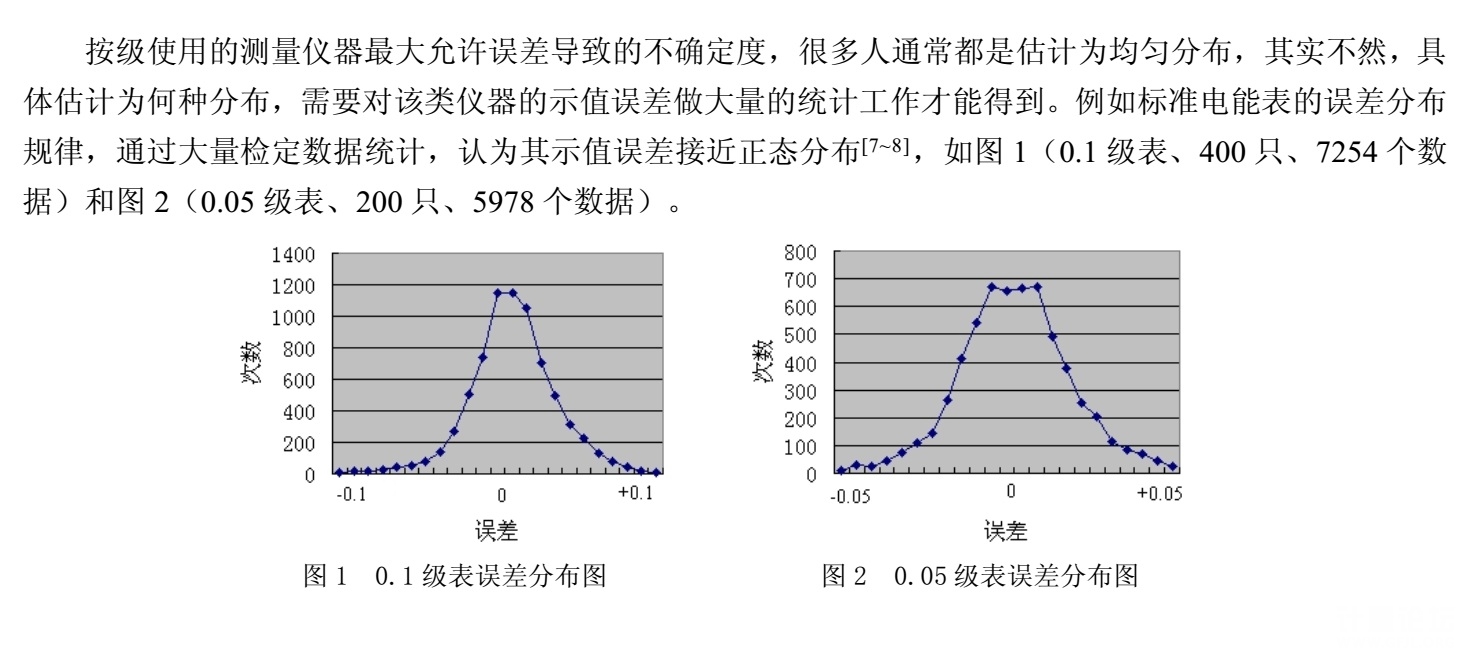
csln 發表于 2018-1-9 15:14
你很個性，明知這不是一回事，偏要但實際上我們是這樣做的。

你怎樣做，同是什么，不是一回事吧

我個人感覺說的挺清楚了=。=整個型號的性能比如MPEV就是一整個型號的性能。另一個個體的性能，單個個體某一時間的具體量值或偏差顯然不是MPEV，但很多時候我們會選用MPEV去估計其具體量值或偏差。因為我們很多時候難以得到單個個體某一時間的具體量值或偏差，或者無需知道那么精確的具體量值或偏差，只需知道單個個體某一時間的具體量值或偏差小于MPEV即可。。

      能知道單臺的時域統計當然用單臺的，但是不知道或者不適用單臺儀器時域統計的時候怎么處理？很多儀器，尤其是電學儀器，在各檢定點根本就很難有一個統一的修正值，這時用“時域統計”工作量將會特別大，根本不具有實用性，“臺域統計”雖然使計量標準的指標看似下降了一些，但至少是一種解決問題的辦法，具有不可替代的作用。“時域統計”只適用于那些適合使用修正值的儀器。

吳下阿蒙 發表于 2018-1-9 13:29
就上面討論的問題，此性能不是彼性能，整個型號的穩定性、量值變化趨勢與單個個體某一時間的具體量值或偏 ...

你很個性，明知這不是一回事，偏要但實際上我們是這樣做的。

你怎樣做，同是什么，不是一回事吧

穩定性偏差又是個什么鬼？

csln 發表于 2018-1-9 11:26
在實際中是存在的，比如一些電阻的老化試驗，一般需要觀測數十個同類型電阻通電數千小時，用以評估整個型號 ...

就上面討論的問題，此性能不是彼性能，整個型號的穩定性、量值變化趨勢與單個個體某一時間的具體量值或偏差是一回事嗎？
這不是一回事，但實際上我們是這樣做的。比如我確認整個型號的穩定性小于某一個值A，那么我評估認為這個型號中的一個單個個體在穩定性實驗的時間內的穩定性偏差小于A，會在每一臺這個型號的單個個體的說明書中標出，其穩定性為A。雖然這個單個個體沒做過穩定性實驗，甚至在后來的測試中發現在時間內它的穩定性偏差大于了A，但也不代表之前的評估有問題吧？畢竟我們不斷的統計現在乃至過去的測量數據，其目的大多數都是為未來服務的，但未來總是存在不確定性的。。

在實際中是存在的，比如一些電阻的老化試驗，一般需要觀測數十個同類型電阻通電數千小時，用以評估整個型號的性能，也就是去評估另一個個體的性能。

我認為您混淆了一個概念，整個型號的性能與另一個個體的性能，就上面討論的問題，此性能不是彼性能，整個型號的穩定性、量值變化趨勢與單個個體某一時間的具體量值或偏差是一回事嗎？整個型號您考察的群體中的某一個個體某個時間的量值同您沒有考察的“另一個個體”某一時間的量值有直接的關系嗎？

您考察的整個型號的這個性能僅能反應一個個體的這個性能而不能反應個體的另外一個性能

csln 發表于 2018-1-9 10:13
這個我清楚，我的意思是，觀測數百個同類儀器的半年后的誤差，用以評估另一臺半年后的偏差。即從一個整體 ...

工廠內的觀測總樣本是同一個型號的所有儀器，很多性能不可能做到直接測量考核“樣本”、“個體”就好了。 觀測數百個同類儀器的半年后的誤差，用以評估另一臺半年后的偏差。在實際中是存在的，比如一些電阻的老化試驗，一般需要觀測數十個同類型電阻通電數千小時，用以評估整個型號的性能，也就是去評估另一個個體的性能。也就是說，目的并不是“一定的樣本”。
而都成先生的文章“擴展不確定度評定中包含因子的確定探討”（《計量技術》2015年第8期）中，中的目的我認為也不是為了反應“一定的樣本”，而是希望反應更多的個體的性能。

吳下阿蒙 發表于 2018-1-9 09:36
某種或某類儀器不長時間內群體誤差分布與個體使用時的時間域誤差沒有什么直接關系
這個我清楚，我的意思 ...

這個我清楚，我的意思是，觀測數百個同類儀器的半年后的誤差，用以評估另一臺半年后的偏差。即從一個整體里面挑選一定的樣本觀測，然后評估整體中某一臺，是很常用的方式。

不明白您這樣做的意義是什么？我寧愿直接去測量、考核這一臺的偏差，就算測量一年也比觀察不太相干的數百臺有效率、有意義，如果這數百臺中就包含您想評估的那一臺，就更明白您想做什么了

如果目的是為了“一定的樣本”或者“個體”，直接測量考核“樣本”、“個體”就好了

這種統計的意義4#說得很明白了

csln 發表于 2018-1-9 08:28
簡單說，那根本就不是一回事，某種或某類儀器不長時間內群體誤差分布與個體使用時的時間域誤差沒有什么直 ...

謝謝，理解了。
我的意思是，觀測數百個同類儀器的半年后的誤差，用以評估另一臺半年后的偏差。即從一個整體里面挑選一定的樣本觀測，然后評估整體中某一臺，是很常用的方式。您的例子中，假設有數百臺完全相同的0.05級標準電能表，并在相同的條件下經過了半年，然后統計這數百臺的每一臺在您需求的那個測量點的偏差值，然后做出分布，那么是可以估計某一只標準電能表此時的實際誤差的。
這和拋骰子那樣，經過觀測統計后，我可以得出使用相同類型的骰子拋出的值的概率是均勻分布，除非你此時使用的骰子或者別的條件和統計時有區別。也就是，電能表的統計并非理想的實驗模型，可能造成最終評估結果的偏差。

如果對一類儀表抽樣的每一個樣本做較長時間比如數個月內單個樣本的誤差分布作統計，進而對這類儀表作時間域誤差分布統計，對這類儀表使用時MPEV貢獻的不確定度分量的分布估計是有意義的，僅靠檢定的數據統計對不確定度評定的分布估計無任何參考價值正如您說的這句。
某種或某類儀器不長時間內群體誤差分布與個體使用時的時間域誤差沒有什么直接關系，這個應該不需要討論吧=。=！不然儀器還做啥長期穩定性觀測。。。數百臺此時的校準檢定合格，也不能說明某一臺明年是合格的。。。但如果我觀測數百臺，確認它們明年的合格率，我是可以評估同類型的某一臺明年合格的概率分布的。。。當然前提是，類型和使用條件等大致相同。。

吳下阿蒙 發表于 2018-1-8 17:43
這就好比拋一個骰子，想要確認其落地是的點數和分布。統計幾百次拋骰子的數據后，可以得出一個點數的分布 ...

簡單說，那根本就不是一回事，某種或某類儀器不長時間內群體誤差分布與個體使用時的時間域誤差沒有什么直接關系

吳下阿蒙 發表于 2018-1-8 17:43
這就好比拋一個骰子，想要確認其落地是的點數和分布。統計幾百次拋骰子的數據后，可以得出一個點數的分布 ...

你這個比喻不恰當， 最后不應該選擇一個  不同于之前類型 的骰子 來說。

csln 發表于 2017-12-12 16:16
已知一只0.05級標準電能表，經檢定合格，且某一測量點檢定時實際誤差為0.02%。問這只標準表檢定后使用了6個 ...

這就好比拋一個骰子，想要確認其落地是的點數和分布。統計幾百次拋骰子的數據后，可以得出一個點數的分布。但拋骰子是理想的實驗模型，而電能表這個卻有非常多的未知區別條件，數百次的電能表統計無法反應單一一個電能表的偏差。好比我統計了幾百次理想骰子的數據后，我拿出一個六個面重量不均等的骰子投擲，那么之前的統計是毫無意義的。請問前輩是這個意思嗎？

已知一只0.05級標準電能表，經檢定合格，且某一測量點檢定時實際誤差為0.02%。問這只標準表檢定后使用了6個月時，這個測量點的實際誤差是多少？那路神仙能知道？

正常人只能知道這時實際誤差可能在正負0.05%范圍內任何一個地方，所以若要評定由其引入的不確定度，合理地按均勻分布處理

試問大神能依據以往的統計數據（除了這只表長期考察數據）確切知道這只表特定時刻實際誤差是多少嗎？又或者知道其呈什么分布嗎？

chuxp 發表于 2017-12-11 13:06
可能這種實驗結果與實驗涉及的儀器密切相關，我覺得大多數情況下，很難確定一定是什么分布。
      ...

-
                             臺域統計出錯；時域統計正確簡單
-
                                                                                                         史錦順
-
       本樓主帖的主題，不是“臺域統計”意義上的分布規律，而是用一個不確定度體系的信奉者都成先生的實驗，來否定不確定度體系的理論和作法。重點是否定“臺域統計”的統計方式。這里再進一步，指出：測量計量的統計方式應該是時域統計，既正確又簡單。
-
（一）臺域統計方式之下的兩種分布之爭，都成正確
       人們都知道，按不確定度評定的一套方式處理問題，例如誤差合成問題，要先將儀器的誤差范圍指標值轉化為不確定度值。所謂B類不確定度評定，常規的作法，就是MPEV除以√3 。這樣做，其前提是儀器的MPEV是均勻分布。只有均勻分布，其包含系數k才是√3。規范GUM、VIM、JJF1059、JJF1001以及大量樣板評定都這樣說，大家也就跟著這樣說，這樣做，習以為常，似乎儀器的誤差分布都是均勻分布。
       都成實驗的意義在于，否定了“儀器誤差均勻分布”的說法。實驗表明，對電能表來說，“誤差是正態分布”。這是實驗，是事實。在臺域統計的框架下，都成的“正態分布說”是正確的。
-
（二）“臺域統計”對通常的測量計量場合不適用
2.1 臺域統計的適用場合
        臺域統計，僅適用于多臺儀器同時測量一個量的情況。工廠生產一批儀器，要分析這批產品的性能，抽一部分樣品（例如20臺）測量，各臺誤差不同。求誤差對各臺的分布，這就是“臺域統計”。
        一般的測量計量，是用一臺儀器重復測量一個量。統計規律是對“時域”而言的，統計方式必須是“時域統計”。
-
2.2 臺域統計方式下，不同分布產生的矛盾現象
       都成用“除以3”、“乘以3”的作法代替原來的“除以√3”“乘以2”的作法，包含概率由95%變成99%. 這可是巨大的變化。這就說明不確定度體系的原有的B類評定方法，并不是普適的，就要重新考慮不確定度評定的一般方法問題。總得給初學者一個交代：該怎樣進行B類標準不確定度評定？似乎話好說：評定者先認定所要處理的儀器的誤差分布規律，再評定。讓每個人去認定要評定的儀器的誤差分布規律，是行不通的。或者說，最不利的情況是均勻分布，按最不利的情況處理。但這就要給出這樣估計對實際情況的偏差有多大。要分析得失情況。例如儀器的MPEV是3%，就是以99%的概率包含真值的區間的半寬是3%. 任務要求的包含概率是99%. 按“均勻分布”，除以√3，變到U時要乘以3，就是變換使MPEV擴大1.73倍，于是包含真值區間的半寬變成5.2%.
       3%變成5.2%，損失太大。這是方法問題。不確定度評定的方法不行！
-
       都成的實驗，對不確定度評定的慣例，有否定意義。但這種“正態分布”，怎么用？都成的除以3、乘以3，似乎可以自圓其說。但如果要求是95%的包含概率，該如何算？如果按都成的辦法，除以3，而乘以2，則MPEV的作用縮小至0.66倍，則包含真值區間的半寬是2%. 明明給出的條件是3%，卻變成2%， 這行嗎？太虛夸了，沒法用。
-
       原來，不確定度體系的問題，不單單是分布的認定問題。而是統計方式的問題。本來計量、測量是用一臺儀器重復測量一個量，而不是用多臺儀器同時測量一個量，因此適應于多臺儀器同時測量一個量的“臺域統計”，根本就不能用在測量計量的單臺儀器重復測量的情況。因此，都成的實驗，既否定了“均勻分布”，也否定了臺域統計的“正態分布”。都成的實驗，否定了自己的作法。
-
（三）簡單、正確的時域統計
       遠在二百年前，高斯對誤差分布，已經有精確的分析和完美的表達。任何測量儀器，只要是給出準確度指標并且是合格的，則其誤差必定是“有偏正態分布”。
       誤差分兩類，一類是恒值，表現為鐘形線對真值的偏離，稱“偏倚”，就是恒值的系統誤差。一類是隨機變量，就是隨機誤差，其特征量是σ。用貝塞爾公式，可以求得σ。
       在誤差理論的意義下，統計是時域統計，分布是“有偏正態分布”。隨機誤差有隨機性，但系統誤差的特點是“恒值性”。在統計時段內（幾秒到幾小時），系統誤差為恒值，沒有問題。在處理誤差合成問題上，誤差的作用時間要求是極短的，就是說統計時段內是恒值，則系統誤差即可按恒值處理。至于系統誤差的長期變化，用長期穩定度表達，而對合成方法沒有影響。
-
       不確定度體系是“方差路線”，但恒值的系統誤差的方差是零。取方差則必然忽略系統誤差的存在與作用。形式上，不確定度體系，為系統誤差加“分布”外衣，但用的是“臺域統計”，與測量計量的一臺儀器重復測量一個量，情況不對，是統計方式錯誤。臺域統計的任何分布，都不能用于時域測量的統計分析。不確定度體系的方差路線是走不通的。
-
       測量計量統計作用的時域性，決定統計方式必須是時域統計。
       時域統計必須兼顧誤差的隨機性與恒值性，就是必須既能適應隨機誤差，也能適應于系統誤差。其方法是著眼于“方根”，對誤差量，取平方，再開方，以實現“絕對值”化。兼顧誤差量的上限性特點，取最大的可能值。
-
（四）誤差理論與不確定度體系的比較

    學術派別               不確定度體系（GUM）                             誤差理論（史法）
    --------------------------------------------------------------------------------------------------------------------------
    統計方式               臺域統計                                                  時域統計
    --------------------------------------------------------------------------------------------------------------------------
    路線圖                   確定分布，一律取方差                             一律取方根
    --------------------------------------------------------------------------------------------------------------------------
    關卡的難易            認知特定儀器的分布規律，難。               “有偏正態分布”是普適的。   
                                 認定相關系數，沒法。                             認定大系統誤差項，容易。
    --------------------------------------------------------------------------------------------------------------------------
    要點                      臺域統計，不適應測量計量。                    時域統計，符合誤差統計規律 。
                                 要認定特定對象的分布規律。                    高斯分布是普適的，不必另求。
                                 取方差，抹煞系統誤差的作用。                 取方根，兼顧隨機誤差與系統誤差。
                                 假設不相關，多數不成立。                        著眼交叉系數，與相關性無關。
                                 混淆手段與對象，一筆混沌帳。                 理論簡單，操作方便，結果清晰。
    ---------------------------------------------------------------------------------------------------------------------------   
-

如果對一類儀表抽樣的每一個樣本做較長時間比如數個月內單個樣本的誤差分布作統計，進而對這類儀表作時間域誤差分布統計，對這類儀表使用時MPEV貢獻的不確定度分量的分布估計是有意義的，僅靠檢定的數據統計對不確定度評定的分布估計無任何參考價值

這是同一個“計量標準”得出的數據，怎么能算是“臺域”，換一個性相近的 “計量標準”再檢定這些標準電能表，結果會有左右偏移。如下圖：

chuxp 發表于 2017-12-11 13:06
可能這種實驗結果與實驗涉及的儀器密切相關，我覺得大多數情況下，很難確定一定是什么分布。
      ...

贊成您的觀點，感覺把這種統計和誤差分布同不確定度評定時的分布聯系起來不可理解，哪兒跟哪兒的事啊，胡亂聯系

比如一批晶振，其中一部分經測試老化率為正，所以出廠時調整到負的MPEV附近，這部分晶振出廠使用若干時間時其誤差分布與出廠時調沒有絕對關系，一批晶振中另外部分更與這一部分出廠調整沒有任何關系，其他儀器不確定度評定時誤差分布更與這些晶振風馬牛不相及

        可能這種實驗結果與實驗涉及的儀器密切相關，我覺得大多數情況下，很難確定一定是什么分布。
       與上述實驗結果相似的實驗統計結果估計很多人都見過，各地省院都有水電燃氣表的監督抽查任務，每次匯總結果的時候，很容易就可以統計出來。我也用EXCEL做過類似的圖，幾百臺家用電能表，做圖的目的是觀察這批表的誤差分布情況，看看是否存在社會傳言的“蓄意加快”的情況。實際結果是近似無偏的正態分布，主要測量點誤差的平均值接近于零，表明不存在加速現象。
        但是，過去的機械式電能表確實存在出廠時要求調整誤差為正值的情形，但不是為了多收電費，而是為了確保其使用壽命，因為其特點是越來越慢，出廠時調快一些，則使用時間可明顯延長。如果對這些表統計，結果可能就是有偏正態分布。類似的情況還有以晶振為內部基準的無線電，時頻儀器，這些晶振的老化率大致已知，出廠時一般調整策略總是保持其滿足盡量多年份內不超差。
         

就算是單純“臺域統計”又能說明什么問題呢？某類儀器群體誤差分布與這類儀器單臺使用時時域誤差分布似乎不搭邊吧，某類儀器或某幾類儀器誤差群體分布與其他儀器單臺使用時時域誤差分布有什么關系呢？

獲取"測量誤差"(及其它"不確定量")的"分布規律"，本是一件非常棘手的事情，除了理論上的那些"絕對隨機量"(在某些意境下，大致對應"白噪聲")，沒有人可能提供普遍適用的求取方法，也沒有人能說自己獲得的某種(個)"結論"絕對正確。  對于其中許多"成份"本來就是"人為隨機"(---基于技術或經濟方面的原因，放棄對相應"規律"的追求)的所謂"系統測量誤差"，其概率分布與測量儀器的實際使用情況密切相關，離開"適當假設"，沒有人能得到可以信服的"分布規律"。   不是靠兩個"獨創"的名詞就能了然的事！  400只/7254個數據，200只/5978個數據，這會單純是您所謂的"臺域統計"嗎？  我以為，您當前對所謂"隨機量"的認識過于"絕對"、狹隘了，所對立的，不僅是"不確定度"，還殃及了"誤差理論"。